Léona Henryson (graphiste et blogueur avec plus de 10 ans d’expérience) enquête sur ce que les designers ne savent peut-être pas influence des mathématiques sur le design.
Si vous demandez à un professionnel de la conception s’il est considéré comme bon à matematiques, la plupart diront non. C’est parce que de nombreuses personnes cherchant à s’adonner à l’art pensent que les compétences requises pour l’art et le design n’ont aucun rapport avec celles liées aux mathématiques.
Ce que beaucoup de gens ne savent pas, c’est que les mathématiques font partie intégrante du design. En fait, de nombreux concepts tels que les modèles, la symétrie, l’espace positif et négatif, les arrangements et les séquences qui sont si importants dans la conception ont des fondements mathématiques.
Même si vous avez fui matematiques Parce que vous considérez qu’ils ne sont pas liés à la partie artistique de l’homme, vous vous trompez et ils sont bien plus utiles que vous ne le pensez, car leur influence est si parfaite qu’ils n’ont pas seulement la fonction esthétique de la perfection et de l’harmonie de l’image , mais aussi le pouvoir d’influencer psychologiquement et bien sûr de communiquer.
Ici, nous partageons le principaux concepts mathématiques que tout concepteur devrait connaître.
séquence de Fibonacci
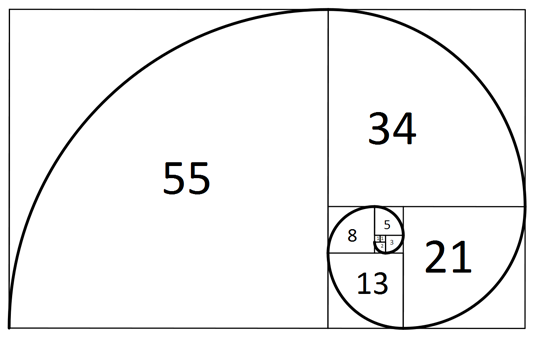
Jouons à un petit jeu. Regardez la séquence de nombres suivante et essayez de déterminer quel nombre est le suivant : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …
Si vous pensiez 89, vous avez tout à fait raison. Le motif de ces nombres est une suite de Fibonacci. Regardez à nouveau les chiffres. Chaque nombre après seize est la somme de deux nombres avant. Pour démarrer une séquence de Fibonacci, il vous suffit de « planter » la séquence avec un numéro de départ puis de doubler le numéro pour démarrer le motif.
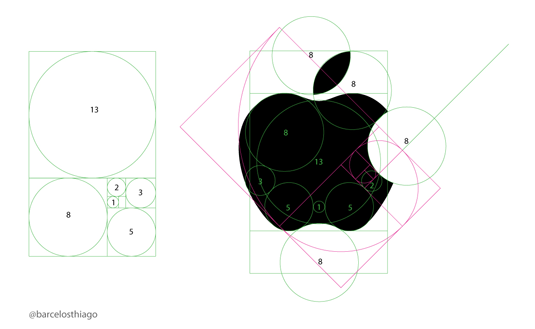
La conception du logo d’Apple utiliserait le nombre d’or
Vous vous demandez probablement ce que cela a à voir avec l’art. Lorsque ces nombres sont traduits en formes, divers motifs émergent, notamment des spirales, des fleurs et des branches. Ces formes peuvent être vues dans la nature et l’art.
En effet, une fois la séquence de Fibonacci découverte, ces nombres ont été divisés en chiffres si proches de zéro qu’ils pouvaient former un diamètre, qui est la base de la spirale suivante.
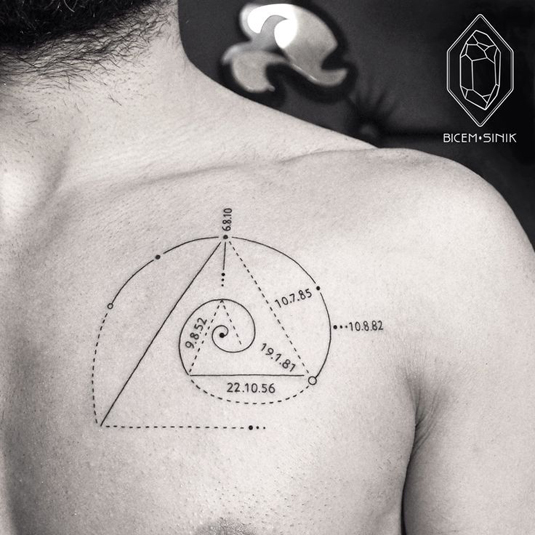
Les spirales, comme vous le savez, apparaissent assez souvent dans la conception. Placés différemment, les nombres de Fibonacci forment la base des étoiles et de nombreuses autres formes géométriques. Même le visage humain suit de près ce modèle.
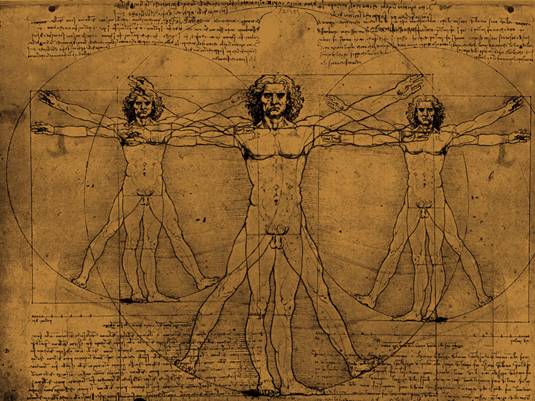
Léonard de Vinci a incorporé le nombre d’or dans son travail
L’architecture historique comme les pyramides de Giiza et le Parthénon contient également une séquence de Fibonacci si vous les examinez de près. Pour en savoir plus sur la façon dont les modèles de nombres ont influencé l’art, vous pouvez faire une petite recherche sur l’art de Léonard de Vinci. Il est bien connu pour son incorporation du nombre d’or dans son travail.
Fractales

Les fractales sont des suites mathématiques
Les fractales sont des motifs géométriques qui se répètent et forment un tout. Dans la nature, les fractales forment des feuilles, des flocons de neige, des structures géologiques et des cristaux de glace. Vous pouvez même couper une orange et voir comment les formes se répètent dans sa pulpe. Ce sont aussi des fractales.

Les fractales apparaissent fréquemment dans la nature
Lorsqu’elles sont examinées au microscope, les cellules humaines sont également constituées de minuscules fractales répétitives. Les scientifiques peuvent utiliser des ordinateurs et des formules mathématiques pour créer des modèles de presque tout en se basant uniquement sur des fractales. Tout ce dont ils ont besoin, c’est de la forme de la fractale à sa plus petite taille, puis de la multiplier.

Les concepteurs utilisent des fractales dans tout, des vêtements aux papiers peints. Les zigzags et les motifs cachemire sont deux exemples de la façon dont les fractales peuvent être transformées en un dessin de toute sorte. Voici un exemple de la façon dont les fractales sont utilisées à des fins de conception.
Comme nous pouvons le voir, les mathématiques peuvent être appliquées dans n’importe quel domaine, même aussi artistique que la conception de sites Web. De nos jours, de nombreux artistes ne s’appuient que sur leurs visions plutôt que sur des mesures lorsqu’ils travaillent sur leurs projets de conception. Laissons de côté le mythe selon lequel les artistes sont mauvais en chiffres et commençons à les utiliser pour améliorer notre travail.
Canon Polyclète

Polykleitos était un célèbre sculpteur grec. En fait, il est largement considéré comme l’un des pères du style grec classique de la sculpture vu dans de nombreux musées à travers le monde. Vos contributions ne s’arrêtent pas là. Il a également écrit un Canon sur la symétrie concernant la sculpture de la forme masculine. Ce canon représentait ses réflexions sur l’esthétique et la perfection artistique.
Il croyait que toutes les parties du corps qui apparaissaient dans une sculpture devaient être clairement distinctes les unes des autres et fournies à l’aide de mathématiques. Par exemple, la taille et la proportion de la première phalange du petit doigt serait la base pour laquelle la proportion du reste du doigt, le doigt serait la base de la proportion de la paume de la main, et ainsi de suite.
Cela a été fait en traitant le bout du doigt comme une unité de mesure carrée. Son travail pour déterminer les meilleurs moyens d’atteindre un équilibre parfait dans la sculpture reste influent aujourd’hui. En fait, le fils et homonyme de Polykleitos a grandi pour devenir un architecte célèbre. Il est difficile d’imaginer que le travail de son père en proportion ne l’a pas beaucoup influencé.
Polyèdres

Un polyèdre est une structure tridimensionnelle constituée d’un ensemble de polygones reliés le long de leurs bords.
Les polyèdres sont intégrés à l’art et au design depuis des siècles. Par exemple, la peinture de Salvador Dalí La Dernière Cène montre Jésus et ses disciples à l’intérieur d’un dodécaèdre, qui est un type de polyèdre. Un réseau polyédrique est un réseau qui a été déplié pour l’impression. Autre œuvre de Salvador Dalí, Corpus Hypercubus utilise un filet polyédrique comme la croix.
Les polyèdres ont été spécifiquement abordés dans le livre Measurement Education écrit par Albrecht Durer. Il était un graveur allemand pendant la Renaissance, qui a écrit le livre pour éduquer les autres sur la perspective. Alors que certaines de ses réflexions sur ce sujet étaient un peu erronées, sa discussion sur les polyèdres et les réseaux polyédriques était assez perspicace.
Ces réseaux contiennent des motifs fascinants que l’on peut souvent voir dans les mosaïques et autres formes d’art où les motifs géométriques sont courants.
Trouver des exemples de mathématiques dans le design et d’autres formes d’art

Même si les artistes et les designers n’utilisent pas de formules mathématiques dans leur travail, les résultats reflètent souvent l’utilisation des mathématiques. Si vous regardez la symétrie, les motifs géométriques, l’équilibre ou les proportions sur un site Web, il y a un principe mathématique derrière ces choses.
Même l’utilisation de l’espace positif et négatif a des origines mathématiques. Ce qui est encore plus intéressant, c’est que ces principes n’ont pas seulement un impact sur les images. Même la façon dont le texte est affiché sur un écran peut impliquer l’utilisation de mathématiques.
Par exemple, le principe selon lequel le texte est plus lisible lorsqu’il y a beaucoup d’espaces blancs est principalement l’utilisation d’espaces positifs et négatifs pour créer quelque chose de plus agréable à l’œil et de plus facile à traiter.
conclusion
Les mathématiques vont de pair avec l’art et le design parce que le cerveau humain apprécie et comprend la cohérence. C’est pour cette raison que la symétrie, l’équilibre, la précision et la proportion sont des éléments si importants d’un design.
C’est aussi la raison pour laquelle les motifs apparaissent fréquemment dans l’art et le design. Si vous avez déjà visité un site Web ou vu une œuvre d’art que vous avez trouvée désagréable et difficile à voir, il y a de fortes chances que l’artiste ou le designer échoue dans l’un de ces domaines.
C’est une chose que cela soit fait par conception, par exemple en peignant quelque chose qui manque de symétrie pour l’effet. Malheureusement, quand c’est simplement le résultat d’une mauvaise exécution, cela devient gênant. Espérons que certaines des informations ici aideront les concepteurs à incorporer des principes mathématiques dans leur travail de plusieurs manières.
Les résultats seront probablement plus esthétiques et plus faciles à utiliser.
tu as aimé ce que tu as lu?
Commentez et partagez avec vos amis
Cela peut vous intéresser :
